Z3 is a powerful framework for problem solving, developed by Microsoft Research. Given a list of restrictions and conditions, Z3 finds one solution that satisfies them all, if that solution exists. Some complex problems can be solved easily with Z3. It can be used for multiple purposes but some known uses in security are exploiting or checking firewall rules. It is also a handy tool for solving many CTF challenges related to encryption and keygen generation.
This is a introductory article, but a technical one. It has the form of a tutorial. It is specially interesting if you want to learn how to use Z3 in Python or you want to get an idea of how Z3 works.
A trivial example of how it would be: I want to find a password that is 8 characters long, and includes, at least, 1 uppercase letter, 1 lowercase letter, 1 digit, and 1 symbol. Letters must be ascii valid. The letters must be at the beginning, then the digit, and then the symbol. In this case, there are many solutions. Z3 will find one, in an efficient way.
It is frequently used for software/hardware verification and testing, constraint solving, analysis of hybrid systems, security, biology , and geometrical problems. Many CTF challenges can be solved with Z3.
In this article I’m going to use the Z3 API in Python. The main source for this post has been this article, but I have explained the concepts and snippets with my own words, added examples, and solved an easy CTF challenge at the end.
Installing Python Z3
Installation is trivial in Linux and if you have a Python environment already:
$ pip install z3-solver
Mathematical examples
Example 1: Declare Ints and solve()
from z3 import *
x = Int('x')
y = Int('y')
solve(x > 2, y < 10, x + 2*y == 7)
First, we import all Z3 functions. Then, Int(‘x’) and Int(‘y’) create two variables, x, and y, in Z3. The sentence, x = Int(‘x’) makes that the Python variable called x points to the Z3 variable called ‘x’. solve() solves the system of constraints. Each parameter passed to solve() is a constraint. In this case, we are using 2 variables, and three constraints.
If we execute this script we get:
$ python example1.py [y = 0, x = 7]
x > 2 → 7 > 2 → True!
y < 10 → 0 < 10 → True!
7 + 2*0 == 7 → True!
Z3 has found an x and a y that make all constraints true. We just told it the constraints, and it found the solution.
Example 2: Real numbers and nonlinear polynomial constraints
from z3 import *
x = Real('x')
y = Real('y')
solve(x**2 + y**2 > 3, x**3 + y < 5)
$ python example2.py [y = 2, x = 1/8]
‘**’ is the power operator.
Example 3: Decimals
from z3 import *
x = Real('x')
y = Real('y')
solve(x**2 + y**2 == 3, x**3 == 2)
$ python example3.py [y = -1.1885280594?, x = 1.2599210498?]
The ‘?’ at the end means the number has been truncated.
Example 4: Unsatisfiable problem
Obviously, there are problems without solution.
from z3 import *
x = Real('x')
solve(x > 4, x < 0)
$ python example4.py no solution
Boolean examples
Z3 supports Boolean operators: And, Or, Not, Implies (implication), If (if-then-else). Bi-implications are represented using equality ==.
Z3 Python API also implements Distinct(x, y, z), which is a shorthand for And(Not(x == y), Not (y == z), Not(z == x)), which means that every element of the list of parameters passed to Distinct() should be different to each other.
Example 5: Boolean example
from z3 import *
p = Bool('p')
q = Bool('q')
r = Bool('r')
solve(Implies(p, q), r == Not(q), Or(Not(p), r))
$ python example5.py [q = True, p = False, r = False]
Implies(p, q) is a constraint that means that if p is True, q is True, but if p is False, q can be True or False. It is the logical implication.
The r == Not(q) is pretty straightforward. The Or(Not(p), r) is a constraint that establishes that p must be False OR r must be True, or both.
Example 6: Helping us with the dress code
from z3 import *
Tie, Shirt = Bools('Tie Shirt')
solve(Or(Tie, Shirt), Or(Not(Tie), Shirt), Or(Not(Tie), Not(Shirt)))
$ python example6.py [Tie = False, Shirt = True]
Tie, Shirt = Bools(‘Tie Shirt’) is a shorthand for:
Tie = Bool('Tie')
Shirt = Shirt('Shirt')
Let’s see the conditions on a table:
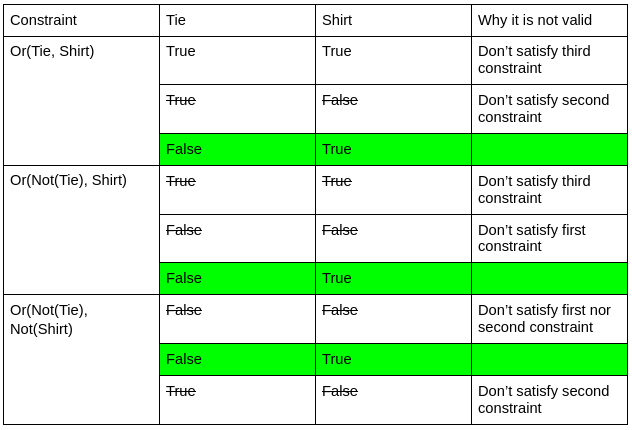
As we can see, Z3 has found the only solution that satisfies the three constraints.
Solvers
We have been passing constraints directly to the solve() method. It is also possible and much cleaner with the problem is more complex, to create a solver and then add to it the constraints, one by one.
To solve a system of constraints added into a solver, we have to first call the check() method on the solver object to determine if the system has a solution; then, we have to call model() to obtain the result.
Example 7: Using a solver explicitly
from z3 import *
x = Int('x')
y = Int('y')
s = Solver()
s.add(x > 10, y == x + 2)
print(s.check())
print(s.model())
$ python example7.py sat [x = 11, y = 13]
List comprehensions
You can use Python list comprehensions to define variables or constraints massively.
X = [ Int('x%s' % i) for i in range(5) ]
This expression creates 5 variables in Z3: x0, x1, x2, x3, and x4. All these variables are stored in a Python list X. X[0] == x0, X[1] == x1, …, X[4] == x4.
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(3) ]
for i in range(3) ]
This expression creates a 3×3 matrix. It creates in Z3 the variables x_1_1, x_1_2, x_1_3, x_2_1, x_2_2, …, x_3_3. They store them in a Python matrix accessible by X[0][0], X[1][0], …, X[2][2].
Exercises
I have extracted these exercises from this article.
Exercise 1: Dogs, cats, and mice
Consider the following puzzle. Spend exactly 100 dollars and buy exactly 100 animals. Dogs cost 15 dollars, cats cost 1 dollar, and mice cost 25 cents each. You have to buy at least one of each. How many of each should you buy?
exercise1.py
from z3 import *
n_dogs, n_cats, n_mices = Ints('n_dogs n_cats n_mice')
s = Solver()
s.add(n_dogs + n_cats + n_mice == 100)
s.add(n_dogs*15 + n_cats*1 + n_mice*0.25 == 100)
s.add(n_dogs >= 1)
s.add(n_cats >= 1)
s.add(n_mice >= 1)
print(s.check())
print(s.model())
$ python exercise1.py sat [n_dogs = 1, n_mice = 14, n_cats = 85]
Easy, huh?
Exercise 2: Sudoku
Something more funny now: solve this Sudoku (with Z3 😎)
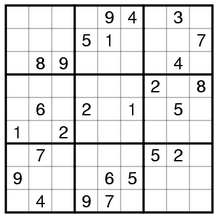
exercise2.py
from z3 import *
X = [ [ Int("x_%s_%s" % (i, j)) for j in range(9) ]
for i in range(9) ]
s = Solver()
# All values on the 9x9 matrix, the sukoku, are integers
# from 1 to 9 included
s.add([ And(X[i][j] >= 1, X[i][j] <= 9) for i in range(9) for j in range(9) ])
# All digits per row and per column must be distinct
s.add([Distinct([X[i][j] for i in range(9)]) for j in range(9)])
s.add([Distinct([X[i][j] for j in range(9)]) for i in range(9)])
# The 3x3 matrices must contain distinct integers
s.add( [ Distinct([X[i + 3*x][j + 3*y] for i in range(3) for j in range(3)]) for x in range(3) for y in range(3) ] )
# Our initial sudoku
# We put 0 on non-defined values to put something
# They will not be on the solution, because we have said that
# the values must be between 1 and 9 included
initial = (
(0,0,0,0,9,4,0,3,0),
(0,0,0,5,1,0,0,0,7),
(0,8,9,0,0,0,0,4,0),
(0,0,0,0,0,0,2,0,8),
(0,6,0,2,0,1,0,5,0),
(1,0,2,0,0,0,0,0,0),
(0,7,0,0,0,0,5,2,0),
(9,0,0,0,6,5,0,0,0),
(0,4,0,9,7,0,0,0,0)
)
# Establish the given value to start, or 0, in Z3 variables
s.add( [ If(initial[i][j] == 0, True, X[i][j] == initial[i][j]) for i in range(9) for j in range(9) ] )
# Check that this has a solution and solve
s.check()
m = s.model()
# Extract the values from the model, and put them into a matrix
# Pretty print the matrix then
r = [[ m.evaluate(X[i][j]) for j in range(9)] for i in range(9)]
print_matrix(r)
What was more difficult for me of this exercise was understanding that what you add is one expression or a list of expressions. Because they are a list, the expression appears between [] like in this line:
s.add( [ Distinct([X[i + 3*x][j + 3*y] for i in range(3) for j in range(3)]) for x in range(3) for y in range(3) ] )
At the end, m.evaluate() is used. This is needed to obtain the solved values from the model. If we had printed X directly, we wouldn’t have seen the results, but the initial definition of X.
CTF challenges
Z3 is frequently used for solving some CTF challenges. Here I’m going to solve one related to crypto which I obtained here.
“My friend has created his own encryption method and is very sure that you can’t crack it without the key. What do you think?
Author: Sud0”
And we get two files:
f=open("flag.txt", "r")
flag = f.read()
g = open("key.txt" , "r")
key = g.read()
key = key[0:4]
def enc(text,key):
encrypted = []
for i in range(int(round(len(text)/4))):
shifted = spicy(text[i*4:(i+1)*4],i,key)
encrypted.append(shifted)
return encrypted
def spicy(text,offset,key):
res = []
for p in range(len(text)):
res.append(int((ord(text[p])+offset)^ord(key[p])))
return res
flat_list = []
for sublist in enc(flag,key):
for item in sublist:
flat_list.append(item)
f=open("enc.txt","w+")
f.write(str(flat_list))
and enc.txt
[28, 24, 1, 9, 9, 19, 93, 93, 94, 2, 26, 13, 6, 92, 61, 11, 15, 39, 91, 91, 20, 28, 54, 8, 17, 89, 23, 61]
The idea is to decrypt enc.txt without, a priori, knowing the key. The algorithm used to encrypt was enc.py and it is supposed to be flawed. Let’s see how the enc.py works.
At the beginning, a file flag.txt is open and read, and its content is stored in flag. As in all CTFs, the flag is what we have to obtain.
f=open("flag.txt", "r")
flag = f.read()
Then, key.txt is open and its content is stored in “key”. However, the next line only gets the 4 first chars of the key! This will be a constraint.
g = open("key.txt" , "r")
key = g.read()
key = key[0:4]
We jump over the two methods defined, by now, and check the rest of the main program. It is pretty straightforward. It seems that enc(flag,key) returns a list of sublists and for each sublist, and for each element of the sublist, the element is appended to a flat_list that is going to be the result stored in enc.txt.
flat_list = []
for sublist in enc(flag,key):
for item in sublist:
flat_list.append(item)
f=open("enc.txt","w+")
f.write(str(flat_list))
Let’s now see the enc(flag, key) method.
def enc(text,key):
encrypted = []
for i in range(int(round(len(text)/4))):
shifted = spicy(text[i*4:(i+1)*4],i,key)
encrypted.append(shifted)
return encrypted
First it declares a list, where it is going to store the result. text contains the flag string.
for i in range(int(round(len(text)/4))):
In this for statement, it gets the length of the flag and divides it by 4 (it makes groups of four, the same length than the key). It rounds the result and enforces it as an int. So, for example, if the flag is 12 chars, this for statement will loop from 0 to 2 (remember that range goes from 0 to the second parameter minus 1). If the flag have 14 chars, it will go from 0 to 2 too, due to the round and int enforcement.
shifted = spicy(text[i*4:(i+1)*4],i,key)
Then it takes each group of four and calls spicy() with these three parameters: the group of 4 chars of the flag, the i, and the full key (of 4 chars too).
| Expression | i | Result |
| i*4:(i+1)*4 | 0 | 0:4 |
| 1 | 4:8 | |
| 2 | 8:12 |
In the end, it seems that the enc() method doesn’t do the heavy work, but the spicy() function does it.
This is the spicy() method:
def spicy(text,offset,key):
res = []
for p in range(len(text)):
res.append(int((ord(text[p])+offset)^ord(key[p])))
return res
In this method, in the variable “text” we have the group of four chars of flag; in offset, the number of the group starting at 0; and in key, the full key. It declares a variable “res” that is a list. There it is going to store the spicy() result. Then, the for loop goes from 0 to the length of text minus 1. As text has 4 chars, it will always go from 0 to 3. And executes this statement:
res.append(int((ord(text[p])+offset)^ord(key[p])))
Let’s review first what ord() and ^ do. The definition for ord() is:
Given a string representing one Unicode character, return an integer representing the Unicode code point of that character. For example, ord(‘a’) returns the integer 97 and ord (Euro sign) returns 8364. This is the inverse of chr.
So, it returns an integer that represents the character. And it is the inverse of chr. So, if we pass a number to chr(), it will return the unicode char. Great!
^ is the bitwise xor operation! Below many encryption algorithms you will find the xor operator. In order to check that is the bit xor operation you can read this. In summary, it is an operation that receives two operators, two bits. Depending on the input bits, the result is different.
| A | B | A ^ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
It does the same with more than one bit, doing the operation one by one:
0101 ^ 1111 = 1010
It has a very important attribute that is crucial for solving this kind of challenges: it is reversible.
So, if A ^ B = C, then C ^ B = A, and A ^ C = B. Which means flag ^ key = enc and enc ^ key = flag, but also, enc ^ flag = key (!)
Now that we have reviewed the ord() and the ^ operators, let’s return to the spicy() method:
def spicy(text,offset,key):
res = []
for p in range(len(text)):
res.append(int((ord(text[p])+offset)^ord(key[p])))
return res
For p between 0 and the length of text (0, 1, 2, and 3), get the int that represents the first char of text and xor it with the ord of the first char of key, convert it to an int and store it on res. Then, return res. So, it is basically a xor, but instead of using the flag char directly, it sums an offset, that is the number of the group (0 to n depending of the size of the flag). The offset is the same for all the chars within the same group or the same call to spicy.
Now we can start writing the constraints for Z3.
The key things to remember is that we know that the plaintext message starts with “pwned{“, because the plaintext is the flag of the CTF, and in this CTF all flags start with pwned{ (his is usually used by easy crypto challenges on the CTFs. In other CTFs the flag starts by flag{, or it can start for whatever prefix they want). With the plaintext and the encrypted text, we can obtain the key, that has only 4 chars.
The key operation is to reverse this:
res[p] == (text[p]+offset) ^ key[p]
To this:
ord(key[p]) = res[p] ^ ord(text[p])+offset
Putting all together, this is the code:
from z3 import *
enc = [28, 24, 1, 9, 9, 19, 93, 93, 94, 2, 26, 13, 6, 92, 61, 11, 15, 39, 91, 91, 20, 28, 54, 8, 17, 89, 23, 61]
# As we want to use the ^ (XOR) operator, we need to use BitVecs
K = [ BitVec("k%s" % (i), 32) for i in range(4) ]
T = [ BitVec("t%s" % (i), 32) for i in range(len(enc)) ]
E = [ BitVec("e%s" % (i), 32) for i in range(len(enc)) ]
text = "pwned{"
s = Solver()
# We add the constraints that the first chars of the plaintext (T) are “pwned{“
for i in range(len(text):
x = ord(text[i])
s.add(T[i] == x)
# Constraints that says that the encrypted vector are enc
for i in range(len(enc)):
s.add(E[i] == enc[i])
# These constraints establishes that the key, that has length 4, are the xor between the for chars one by one of the plaintext and the encrypted text
for i in range(4):
s.add(K[i] == T[i]^E[i])
# These constraints establish the values of the plaintext as defined in the encrypted routine. # We don’t need to reverse the logic, just state what is the restriction
# Z3 will try to comply with all constraints at the same time, and in that process, it will solve the # key and then the plaintext
for i in range(int(round(len(enc)/4))):
for j in range(i*4, i*4 + 4):
s.add(T[j]+i == E[j]^K[j%4])
print(s.check())
m = s.model()
# At this point, the model is solved, but we have the values as BitVecs and we want to see the
# string, so we have to do the conversion. Evaluate accesses the already solved values on the
# model
flag = ""
for i in range(len(T)):
flag = flag + chr(int(str(m.evaluate(T[i]))))
print(flag)
The solved flag is “pwned{100ks_g0Od_D03snT_w0rK”. Flags should end with a ‘}’. I assume that to make it easier they removed it to make the plaintext a multiple of 4, but the correct flag would end with }.
The challenge is easy and probably Z3 is not necessary, as the xor operation and obtaining the key is trivial, but I hope it helped understand Z3 better.
Conclusions
Z3 is a very handy tool that is worth having in your toolbox. It can be used for multiple purposes, not only CTFs. It can be embedded within more generic programs to solve specific problems.
When you understand how it works it can help solve some problems much easier than if you try to define an algorithm. At the end, what you say to Z3 is what you want, the conditions, and it finds a way, in an efficient way.
References
I obtained the explanations, examples, and the CTF challenge from different sources. I put them here and added some more:
https://ericpony.github.io/z3py-tutorial/guide-examples.htm
http://theory.stanford.edu/~nikolaj/programmingz3.html#sec-intro
https://ctftime.org/writeup/29142
https://0fa.ch/writeups/reverse/2020/05/09/reverse-sharkyctf.html
https://github.com/ViRb3/pwnEd-ctf/tree/master/customcrypto
